Uncertainty Visualization by Representative Sampling from Prediction Ensembles

论文：Uncertainty Visualization by Representative Sampling from Prediction Ensembles
作者：Le Liu, Alexander P. Boone, Ian T. Ruginski, Lace Padilla, Mary Hegarty, Sarah H. Creem-Regehr, William B. Thompson, Cem Yuksel, and Donald H. House

发表：IEEE InfoVis 2017

介绍

背景

模拟模型已成为预测生成的主要工具，但这些模型的预测通常包含高度不确定性。这种不确定性可能有很多来源。当被建模的系统由非线性动力学控制时，而且敏感地依赖于初始和边界条件，这是不确定性就会不可避免的发生。其他不确定性来源包括对实际系统建模，参数估计和数值误差累积所做的假设和近似。
集合(Ensemble)是对可能由包含不确定性的模型产生的投影空间进行采样的关键工具之一。在天气预报中使用模型就是一个很好的例子。通常，一次或多次天气模型多次运行，每次运行的初始条件或参数略有不同。这就得到了基于模型的单个投影的集合，气象学家必须从中确定要向公众呈现的聚合预测。通常，这将包括预测的天气结果，以及预测的确定性或置信度的度量。

挑战

虽然集合是进行预测的重要工具，但是它们很难用于创建有效的可视化。

现有的可视化方法

现有的可视化方法有摘要显示(Summary Display)和直接集合显示(Direct Ensemble Display)。

摘要显示

摘要显示可视化方法需要至少显示集合的均值和中值，以及数据传播的一些指示。例如：地图上使用等高线来显示大气压力预测的位置和传播；轮廓箱图可以显示空间轮廓集合中的中值，扩散和异常值；同心置信区间是一种观察飓风预测的方法，该方法通过一组同心置信区间总结了一系列风暴空间位置。
但是，当空间扩散被用作不确定性的指标时，可能导致观察者得出错误的结论。一个典型的例子是美国国家飓风中心（NHC）使用的锥体显示预测的飓风路径及其不确定性，如图 1 所示，锥形表示热带气旋中心的可能轨迹，并且通过沿着预测轨道（在 12,24,36 小时等处）围绕由一组圆圈（未示出）扫过的区域而形成。设置每个圆的大小，使得 5 年样本中三分之二的历史官方预测误差落在圆圈内。椎体的宽度代表 66%的置信区间，这种众所周知的显示导致对风暴大小的误解 – 观众倾向于理解风暴随着时间的推移而增加。此外，观察者的感知可能会因中心线的存在而产生偏差，而显示的二元内外不确定性视图可能导致过高估计锥体内的可能性，并低估锥体外的可能性。而且，一项使用眼动追踪和心理生理学测量的研究表明，通过使用变色和不透明度等方法是不能解决这些问题的，显然这些问题是摘要显示的本质所固有的。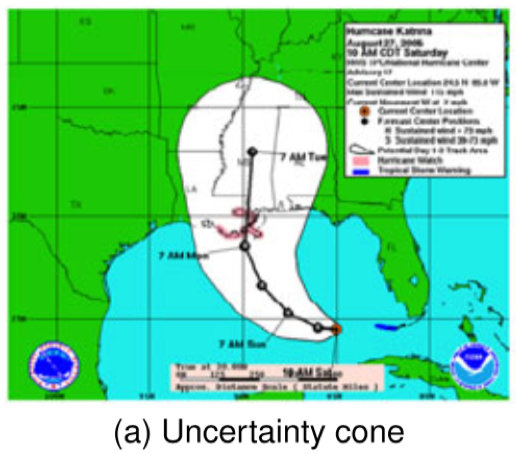

图 1 国家飓风中心的不确定性锥体

直接集合显示

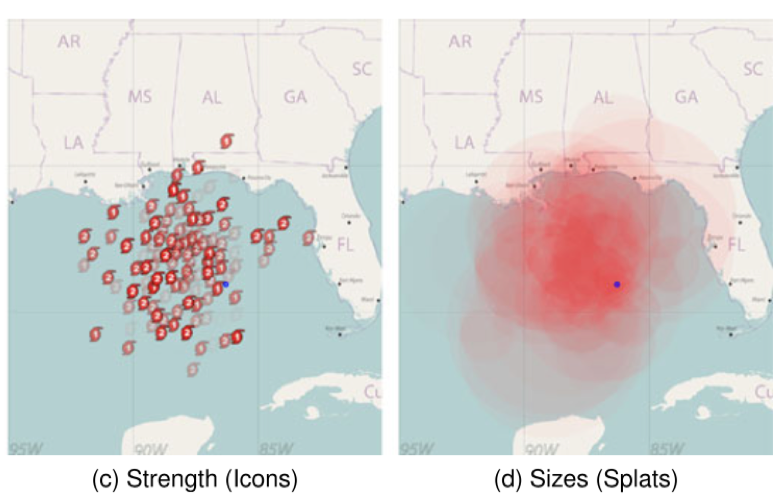
预测集合的良好结构的直接显示可以优于摘要显示，既可以传达与预测不确定性相关的空间分布，又可以最大限度地减少空间属性的混淆。直接集合显示的另一潜在优点是它们降低了显示元素的维度。不是使用汇总区域或体积显示来显示点的集合，而是保持 2D 或 3D 点。同理，路径仍然是线段。而对于点，每个点处可以显示 glyph，可以用于传达关于集合成员的附加信息。例如，在飓风位置显示中，每个集合成员可以由编码飓风类别的 glyph（即，最大风速）表示，如图 2 所示。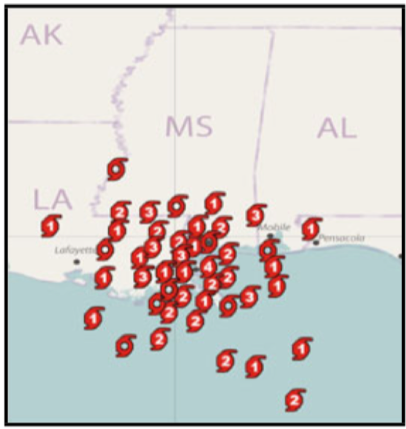

图 2 每一个点由编码飓风类别的 glyph 表示

但是当集合成员过多时，直接显示就会出现一些可视化问题，即视觉混乱、重叠，让用户难以理解。避免这些问题的一种抽样方法是通过蓝噪声采样，其产生一组随机定位但在空间上保持良好分离的样本。蓝噪声采样可以减轻视觉混乱问题，但是不能保证子集与原始分布近乎相同，而且本文作者通过调研发现，现有的采样技术中没有既可以精确保留集合分布，又可以解决遮挡问题。

贡献

本文主要是为了探索当集合是一组点时从预测集合中进行有效显示的方法，做出的贡献有：

开发一种采样技术，该采样技术提取点集合的代表性子集，其不仅准确地保留原始分布，而且还保持子集成员之间的良好空间分离。
开发对通过时间进行采样的飓风预测集合的两个动态可视化。其中一个通过样本点处的字形传达飓风强度，而另一个通过圆圈传达风暴大小，其半径由风暴大小决定。
改进以前的摘要显示，展示了我们的采样技术如何用于支持平滑和精确的插值。
报告认知实验的结果，以比较参与者对集合可视化的理解与现有摘要显示的理解。

数学与算法基础

径向基函数(RBF)插值

RBF 是某种沿径向对称的标量函数。通常定义为空间中任一点 x 到某一中心 xc 之间欧氏距离的单调函数。最常用的径向基函数是高斯核函数，其中 x0 为核函数中心,r 为函数的宽度参数,控制了函数的径向作用范围。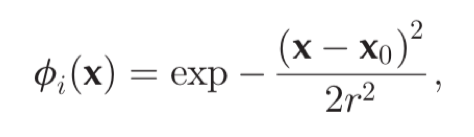

通过正交最小二乘法(OLS)选择子集

仅使用 RBF 进行插值存在问题：大量点样本，过度拟合。
OLS 是一种通过选择一个小的代表子集来解决 RBF 插值问题的方法，用作插值的简化基。OLS 通过选择最小化原始采样点处的 RBF 插值误差平方和（SSE）的样本，以一个空子集开始，一次添加一个点样本。前向选择算法(forward selection algorithm)是该算法的快速实现。

通过加权样本消除(WSE)选择子集

泊松盘采样

与单纯的随机采样方法相比，这种方法在保持随机性的同时，使采样点的分布更加均匀，可以弥补随机采样的不足。

WSE：生成泊松盘样本集的算法

从现有样本集开始，通过算法计算返回半径和指定大小的子集，半径为子集的泊松盘属性。这种算法可以确定空间分布。

采样方法

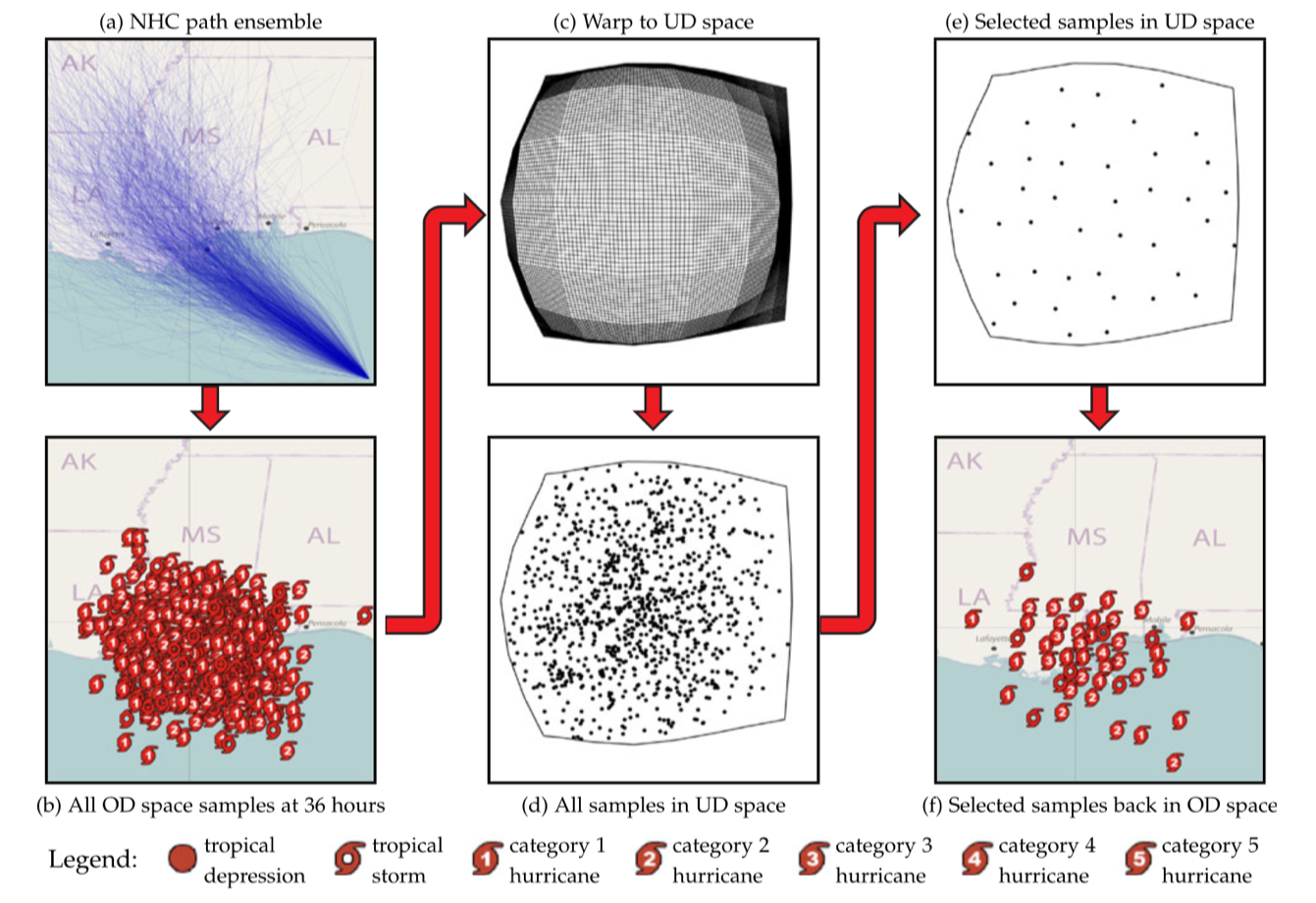
图 3 可视化管道，从路径集合中进行采样，以生成结构良好的特定时间集合可视化

图 3 显示了用于国家飓风中心提供的预测飓风路径集合的方法示例。原始集合（图 3a）在 36 小时内被采样到预测中（图 3b），以显示预测数据中可能的飓风位置。这些是使用标准 glyph 显示的，NHC 用它来表示地图上的飓风地理空间位置和强度。我们构造了一个空间扭曲（图 3c），将地理空间样本集转换为一个均匀分布的空间（图 3d），我们称之为 UD 空间。我们选择样本的子集（图 3e）以在 UD 空间中实现泊松盘分布。最后，选定的点被转换回原始空间（我们缩写 OD 空间）并使用 NHC 字形显示地理空间（图 3f）。
下面介绍从 M 个点的集合中选择 N 个点的代表子集的方法的各个步骤：

确定原始密度(OD)空间中 M 个点的边界区域
所有工作都是针对原始密度（OD）空间中的整体点的边界区域完成的
计算边界区域上的连续密度场

在为每个采样点分配局部数据密度值之后，我们使用径向基函数插值计算样本空间上的密度场。
使用 k 个最近邻（kNN）方法直接作用于原始集合的样本，σi 为密度，ρi 是以 xi 为中心的圆的半径，最小程度的包围了点 i 的 k 个最近邻。这里我们避免使用基于网格的离散化来进行密度估计，因为来自原始集合的输入数据可能以非常不均匀的方式分布，这可能导致采样问题。
使用 OLS 为 RBF 选择小的代表子集，因为点太多，会出现过度拟合问题
RBF 的宽度参数，其中 w 是 OD 空间中边界区域的最大维度，b 是用户可设置的常量。

通过上面的步骤进行采样得到的结果如图 4 所示，子集太均匀，不能很好地表示原始集合的统计特性；子集包含太靠近的点，从而导致遮挡问题。

图 4 在原始空间中使用 OLS 选择的最佳子集分布

解决这个问题的方法是在均匀密度（UD）空间中执行样本选择，即后面要做的工作。 3. 构造从 OD 到 UD 空间的扭曲函数

使用累积密度函数定义从非均匀分布到均匀分布的映射。
高斯-赛德尔样式松弛。根据初值，设定一些参数，算出下一步的结果，得到变形后的网格，并且确保没有网格单元被反转或具有交叉边缘，具体细节可以自己细看。
分层渐进细化方法。为了实现高质量的扭曲功能，我们需要一个高分辨率的网格。但是，当由于网格变形引起的网格顶点的位移远大于网格边缘的长度时，松弛过程可能导致交叉边缘，反转单元并因此改变网格的拓扑结构，从而导致不稳定性。我们首先使用松弛法来计算低分辨率的变形网格。然后，我们细分网格单元并继续对具有更高分辨率的细分网格进行松弛过程。这样，使用较低分辨率的网格处理网格的大变形，并且使用较高分辨率网格的松弛引入变形的精细细节，如图 5 所示。

图 5 用于计算扭曲函数的初始和三级分层细化。

将每个点从 OD 空间映射到 UD 空间
利用上步得到的扭曲函数映射每个 OD 空间中的点(xi,yi)到 UD 空间中的点(ui,vi)，使得 UD 空间中的样本均匀分布。
在 UD 空间中选择一组 N 这一步的采样，可以采用上文中介绍的 OLS 或者 WSE，这两种方法选择具有不同特征的子集。采样结果如图 6 所示，通过 OLS 进行采样得到的子集样本点会集中一些，而通过 WSE 采样得到的自己样本点分布比较均匀，这是由于 WSE 生成的是泊松盘样本集。

图 6 在 UD 空间中通过 OLS 和 WSE 算法选择的样本的比较

将 N 个选定点投射回 OD 空间并显示
由于我们的松弛过程确保没有网格单元被反转或具有交叉边缘，因此对于 UD 空间中的任何点存在唯一的变形网格单元。这里可以利用空间分区结构来快速找到相应的单元。然后，可以使用重心坐标将点投影到相应的未变形 OD 空间单元。

验证

这篇文章根据所做工作进行了以下两项验证：
a. 选择的子集紧密地再现了由全点集合编码的空间分布
b.支持叠加在地图上的两种形式的可视化，点集直接显示与摘要显示
验证采用的数据是 NHC 为飓风艾萨克提供了 1000 条预测路径，下面分别介绍如何对这两点进行验证。

选择的子集紧密地再现了由全点集合编码的空间分布

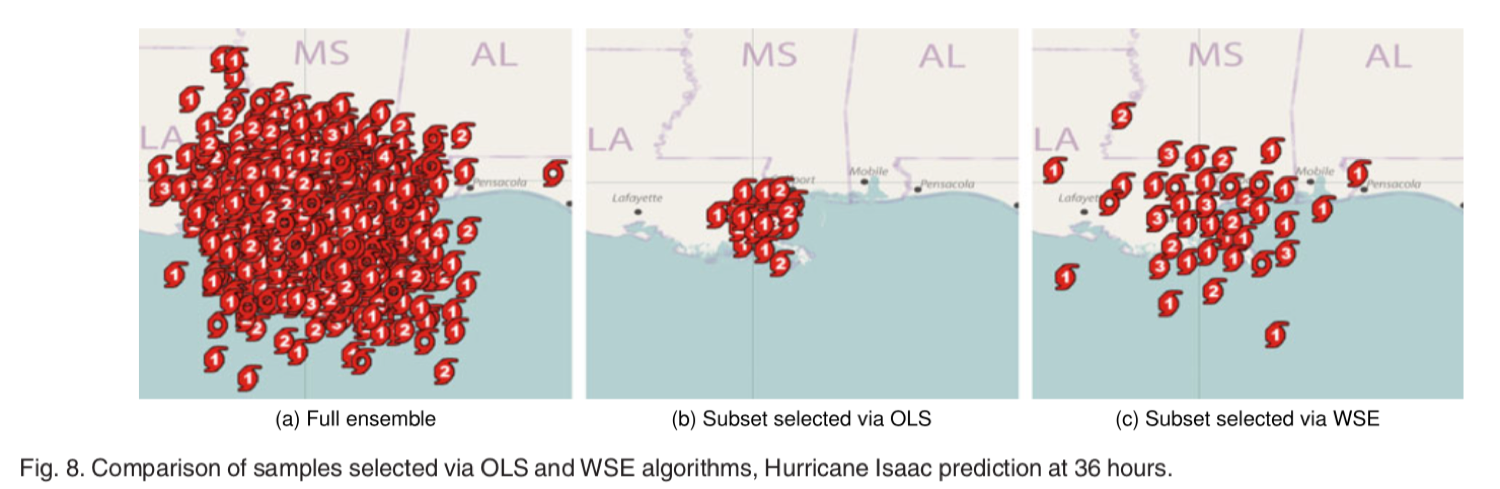
图 7 通过 OLS 和 WSE 算法选择的样本的比较

图 7 展示了通过 OLS 和 WSE 算法选择的样本的比较，可以看到 OLS 的子集较集中，而 WSE 的子集较均匀。值得注意的是，虽然图 7 中的原始集合似乎扩展到比 OLS 和 WSE 生成的两个子集更大的区域，但是远离中心的这些离群值样本实际上出现的概率非常低，由于遮挡，靠近中心的集合样本的密度是完全看不出来的的。因此，完整整体的可视化可能会产生误导。
虽然两种选择算法产生具有不同布局的子集，但两个子集都代表原始集合。验证方法：判断所选子集能否再现原始集合支持的分布。实际操作是从原始点集与每个选定的子集中构建单纯深度场(simplicial depth fields)，由于单纯深度提供了对集合中点的中心性的测量，所以通过比较两个单纯的深度场，我们能够评估子集的代表性。这里将单纯深度值归一化到[0,1]，颜色编码点集样本的显示，如图 8 所示。

图 8 全集以及通过 OLS 和 WSE 算法选择的样本集的单纯深度场比较

得到三者的单纯深度场后，对其进行视觉比较，即从原始集合图像中减去 OLS 和 WSE 图像的灰度值，得到的结果如图 9 所示，可以看到，最大的变化仅为单纯深度值范围的 5％，所以两个选定的子集都高度代表原始样本集，用户可以按照子集的可视化需求进行选择，第一个需要验证的点得证。

图 9 从原始集合图像中减去 OLS 和 WSE 图像的灰度值的结果图

支持叠加在地图上的两种形式的可视化

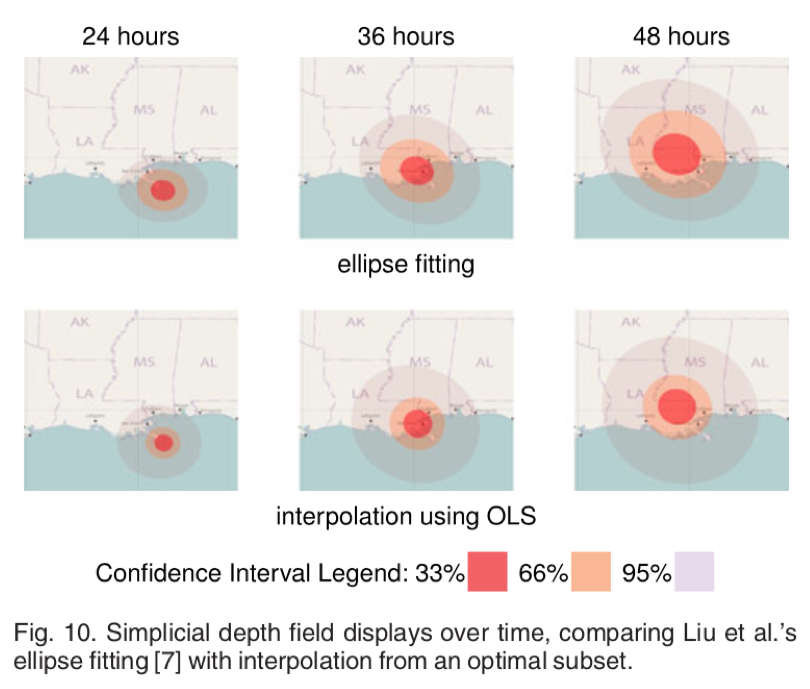
图 10 单纯深度场显示与椭圆拟合的插值比较

图 10 的第一行展示的是已有的绘制摘要显示的工作，采用了椭圆拟合的方法，具有不稳定性。第二行展示的是本文的工作，使用 OLS 选择算法，直接从插值的单纯深度场产生非常相似的可视化，无需求助于椭圆拟合，具有计算效率高，稳定性高的优点。

可视化改进

图 11 两种动态可视化方案

这篇工作向 NHC 的气象学家展示了这些可视化，并根据根据气象学家反馈进行可视化设计的修改，反馈有以下三点：

对可能遇到飓风强风的区域没有足够的覆盖范围
集合的各个元素非常突出，可能误导观众过分关注某些图标符号而不是整体分布
图标符号描绘了一组预测位置，没有显示受飓风强风影响的区域范围

针对前两点反馈，提出了图 11 左的可视化改进方案，即加入不透明度的概念。而针对第三点反馈，提出了图 11 右的可视化改进方案，对样本点的半径进行编码，其半径对应于预测到 50 kn 风的中心的预测距离。这两种可视化方案的动态效果可以参看作者的主页：https://people.cs.clemson.edu/~lel/

实验评估

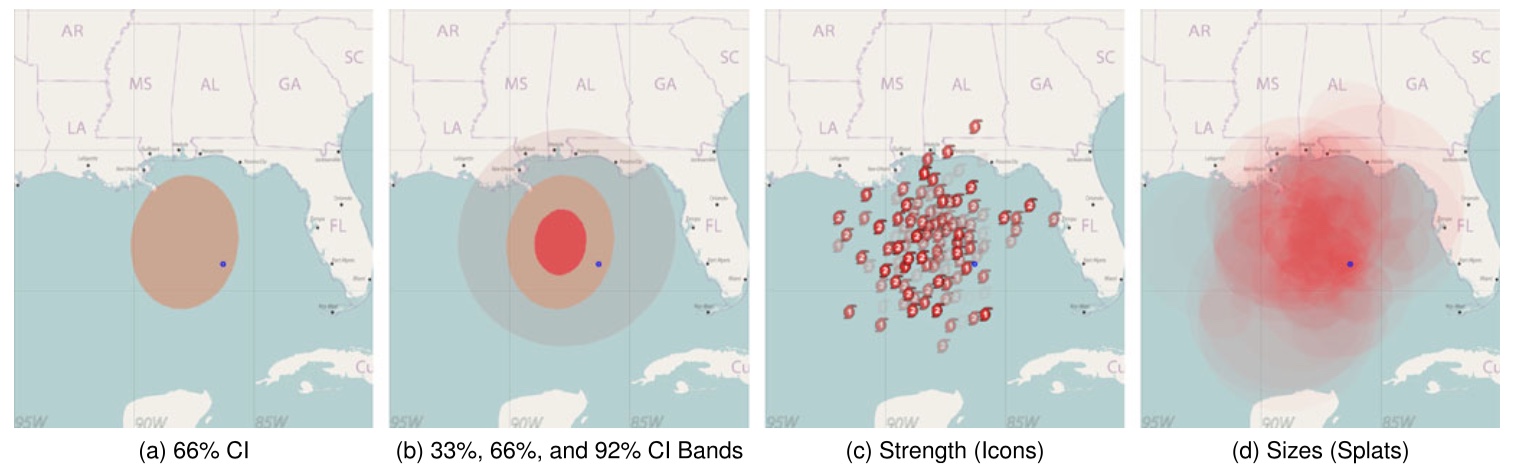
图 12 在认知实验中研究了四种可视化风格。蓝点表示石油钻井平台的位置

来自加利福尼亚大学，圣巴巴拉大学和犹他大学的 133 名参与者
图 12 展示了三种新可视化（后三种）与简单地显示了预期风暴中心的 66％置信区间的可视化（第一种）
首先参与者被随机分配到可视化类型，并提供该可视化的描述和任务说明
参与者被告知有一个石油平台，并指示根据风暴影响平台的可能性和受影响地区风暴的强度来估计平台可能造成的损害程度。范围从 1（无损坏）到 9（严重损坏），参与者输入他们的回答。
评估可视化在帮助用户估计飓风风险方面的有效性。参与者被问到一系列七个真/假问题，以评估他们对可视化的理解，包括误解。

未来工作

探索 OLS 与 WSE 两种算法的混合，选择一个强调布局中心性的子集，同时保持对异常值的高度认识。
研究保留所有信息分布的方法，同时仍然支持良好的空间布局。

Questions & Discussion： ✉️ weiyating@zju.edu.cn